LOOKING    FOR GRISHA

MIGUEL BANDERA RUIZ 

INTRODUCCIÓN

Toda esta introducción me permite ahora presentar un diálogo
entre dos de las figuras más prominentes de la ciencia en
la primera mitad del siglo XX, poniendo énfasis en una discusión
eterna entre la matemática y la física. Aquí va.
Einstein: —Usted sabe, Henri, al principio, yo estudiaba matemática.
Pero la dejé y me dediqué a la física…
Poincaré: —Ah… No sabía, Alberto. ¿Y por qué fue?
Einstein: —Bueno, lo que pasaba era que si bien yo podía darme
cuenta de cuáles afirmaciones eran verdaderas y cuáles eran
falsas, lo que no podía hacer era decidir cuáles eran las importantes….
Poincaré: —Es muy interesante lo que me dice, Alberto, porque,
originalmente, yo me había dedicado a la física, pero me
cambié al campo de la matemática…
Einstein: —¿Ah, sí? ¿Y por qué?
Poincaré: —Porque si bien yo podía decidir cuáles de las afirmaciones
eran importantes y separarlas de las triviales, mi problema…
¡es que nunca podía diferenciar las que eran ciertas(...)

(Matemática ¿estás ahí ? de Adrián Paenza)

CAPÍTULO I

Me imagino a Grisha (Grigori  Perelman), considerado por la prensa sensacionalista como el hombre más inteligente del mundo, aislado voluntaria y arrogantemente del mundo en su casa, en las afueras de San Petersburgo, vestido con un chándal de nike por el que se desparrama su larga barba castaña, sentado en una mesa camilla con una botella de buen vodka y leyendo incansable, a través de sus grandes ojos azules bajo unas pobladas cejas, una tras otra, las miles de cartas que le llegan diariamente de las instituciones científicas más importantes del planeta mientras su madre, con la que vive sólo, le prepara unos aperitivos (zakuska), como antesala a una excelente ensalada de cangrejo (kraboviy salat), a la vez que piensa, discretamente, en los tres factores que han condicionado la vida reciente de su querido hijo: la medalla Fields, la conjetura de Poincaré y su propio carácter.

Todo empezó en 1897, en Zurich, donde tuvo lugar el primer Congreso Internacional de Matemáticos (ICM). Actualmente, las reuniones del ICM  se hacen cada cuatro años; el congreso del año 2002 se celebró en Beijing (China) y el del año 2006 ha tenido lugar con gran éxito en Madrid, siendo la primera vez que viene a España. En el Segundo ICM, celebrado en París en 1900, David Hilbert (23 de enero de 1862, Wehlau, Prusia Oriental-14 de febrero de 1943, Göttingen, Alemania), uno de los matemáticos más influyentes del siglo XX, propuso en la conferencia “Los problemas de la matemática” 23 problemas sin resolver hasta entonces, la recopilación de problemas abiertos más exitosa y de profunda consideración producida nunca por un único matemático. La introducción de la mencionada conferencia fue la siguiente:

¿Quién entre nosotros no estaría contento de levantar el velo tras el que se esconde el futuro; observar los desarrollos por venir de nuestra ciencia y los secretos de su desarrollo en los siglos que sigan? ¿Cual será el objetivo hacia el que tenderá el espíritu de las generaciones futuras de matemáticos? ¿Qué métodos, qué nuevos hechos revelará el nuevo siglo en el vasto y rico campo del pensamiento matemático?

Presentó menos de la mitad de los problemas en el Congreso, que fueron publicados en las actas. Extendió el panorama en una publicación posterior, y con ella llegó la formulación canónica actual de los 23 Problemas de Hilbert. El texto al completo es importante, dado que la exégesis de las cuestiones puede seguir siendo materia de debate inevitable, cada vez que se preguntan cuántas han sido resueltas; algunos se resolvieron en poco tiempo, otros se han discutido durante todo el siglo XX, y actualmente se ha llegado a la conclusión de que unos pocos son irrelevantes o imposibles de cerrar. Algunos continúan siendo actualmente un reto para los matemáticos.

En conmemoración de los 23 célebres problemas propuestos por Hilbert, el 24 de mayo del 2000, también en París, el Clay Mathematics Institute, de Cambridge (Massachussets) anunció siete premios de un millón de dólares cada uno a quienes resolviesen, a satisfacción de la comunidad matemática internacional, siete célebres problemas matemáticos (“Los problemas del Milenio”) que permanecían sin solución en esas fechas y que, a juicio de un selecto comité de profesionales, estaban entre los más difíciles e importantes en ese momento. En el comité figuraban Arthur Jaffe (Harvard), que fue presidente de la American Mathematical Society y actualmente presidente-fundador del Clay M. Institute, y los medallas Fields, Michael Atiyah (Cambridge), Edward Witten (Princeton)   y Alain Connes (París); entre los proponentes de problemas concretos figuraban, además, los conocidos matemáticos Enrico Bompieri, John Milnor y Andrew Wiles (que demostró el llamado “último teorema de Fermat”). En diversos lugares del mundo, y en particular en la Universidad de Texas en Austin, se celebró el acontecimiento con numerosas conferencias por especialistas sobre todos estos problemas. Las conferencias de Texas pueden consultarse en video on line en la dirección                                                                                         

http://www.claymath.org/annual meeting/2000 Millennium Event/Video/

En una reunión de la Real Academia de Ciencias de Zaragoza en octubre de 2003

se acordó que la Academia organizase unas conferencias donde especialistas nacionales

explicarían al público científico universitario zaragozano el significado de esos problemas y el estado actual de su posible solución; a esos efectos la Sección de Matemáticas de la Facultad de Ciencias de la Universidad colaboró activamente con la Academia en la selección de los conferenciantes y en el acceso a los mismos. La conferencia final en Zaragoza corrió a cargo de María Teresa Lozano, de la propia Universidad y Académica, una especialista mundial en la Conjetura de Poincaré, el Problema Cinco (Clay M. Ins.).

CAPÍTULO II

MEDALLA FIELDS

TRANSIRE SVVM PECTUS MVNDOQUE POTIRE

El 27 de noviembre de 1895, Alfred Nobel –inventor de la estruendosa dinamita- dejaba su gran fortuna, cifrada en más de 30 millones de coronas suecas, a una fundación benéfica con la misión de conceder premios anuales a todos aquellos que hubiesen mejorado la vida de sus congéneres desde sus diferentes campos de investigación profesional. De ese modo, nacieron los renombrados premios Nobel en homenaje a su creador. Sin embargo, entre los consabidos galardones en Física, Química, Medicina y Fisiología, Literatura y a favor de la Paz (a los que después se sumó el de Economía), muchos echaron en falta un reconocimiento a la imprescindible ciencia matemática. Según las malas lenguas, esta exclusión se debió a que el célebre inventor sueco no quiso incorporar dicha distinción a la nómina de premiados por el odio que sentía hacia Gösta Mittag-Leffler. Éste era un prestigioso matemático escandinavo que tiempo atrás había mantenido algún escarceo amoroso con la novia de Alfred Nobel. De esta forma se habría vengado de su molesto rival y más que posible premiado de haber constituido la categoría de matemáticas entre sus premios.

Para solventar este injusto vacío en el reconocimiento de los hechos científicos más destacados, en el Congreso Internacional de Matemáticas de 1924, celebrado en Toronto y presidido por John Charles Fields, gran matemático canadiense, se presentó la propuesta de unas medallas para premiar los trabajos más importantes en el campo de la Matemática . La primera concesión de medallas tuvo lugar en el Congreso de Oslo de 1936, cuando el rey Haakon VII de Noruega entregó la primera al matemático finlandés Lars Ahlfors,  interrumpiéndose en los años 1940 y 1944 por el conflicto bélico mundial, y no reanudándose, por motivos de organización, hasta 1950 ; desde entonces, se han concedido los premios cada cuatro años, ininterrumpidamente, hasta completar, con las medallas del 2006, un total de 46 galardonados.

Siguiendo escrupulosamente una regla no escrita, se concede sólo a matemáticos de menos de cuarenta años y en cada congreso se otorgan habitualmente cuatro medallas, nunca más de cuatro, sin superar el ritmo de una por año. Finalmente la cuantía de la medalla Fields es puramente simbólica comparada con la del Nobel.

Las medallas, que están acuñadas en oro, fueron diseñadas por el escultor canadiense Robert Tait Mckenzie y las inscripciones redactadas por el profesor G. Norwood, de la Universidad de Toronto; en el anverso aparece la inscripción latina "TRANSIRE SVVM PECTUS MVNDOQUE POTIRE" (sobrepasar su propio entendimiento y apoderarse del mundo) junto al busto de Arquímedes y su nombre en griego; en el reverso figura la inscripción "CONGREGATI EX TOTO ORBE MATHEMATICI OB SCRIPTA TRIBVERE" (reunidos los matemáticos de todo el mundo para premiar las obras maestras), junto con el dibujo del gran Arquímedes.

El jurado de los premios es designado, entre dos congresos consecutivos, por el comité ejecutivo de la Unión Matemática Internacional, y su composición se mantiene en secreto hasta la concesión de las medallas.

Este año, el XXV International Congress of Mathematicians (ICM2006) se ha celebrado, del 22 al 30 de agosto, en Madrid tal y como se aprobó en la asamblea general del Comité Internacional de la IMU celebrada en Shanghai en 2002 durante la celebración del anterior congreso en Pekín (que contó con la asistencia de 4270 matemáticos de 101 países). Constituyen el mayor acontecimiento científico y social de la comunidad matemática internacional, siendo la entrega de las medallas Fields, y los premios Nevanlinna y Gauss, uno de sus momentos culminantes.

John Ball, presidente del Comité de las Medallas Fields, dio a conocer los galardonados en este Congreso y S. M. El Rey Don Juan Carlos entregó las medallas Fields:

Además, el estadounidense Jon Kleinberg, de 35 años, recibió el premio Nevanlinna por sus trabajos sobre la Sociedad de la Información e Internet, y el japonés Kiyoshi Ito, de 90, el premio Gauss por sus trabajos sobre modelos de sucesos aleatorios.

CAPÍTULO III

LA CONJETURA DE Poincaré

Henri  Poncaré (1904):

“Toda variedad de dimensión 3 cerrada y simplemente conexa es homeomorfa a la esfera de dimensión tres”

¡POR FAVOR, NO CIERRE LA PÁGINA. TRATARÉ DE EXPLICÁRSELO LO MEJOR POSIBLE!.

El enunciado no pudo ser resuelto durante un siglo y su demostración fue considerada uno de Los siete problemas del Milenio propuestos por el Clay Mathematics Institute.

En noviembre de 2002 corrió el rumor en Internet de que Grigori Perelman (“Grisha”) había publicado en arXiv una solución a la Conjetura; arXiv es un sistema electrónico y automático de distribución de artículos de investigación (preprint) en diversos campos (física, matemáticas, etc.) sin revisión editorial, lo que reduce ampliamente el coste.

En efecto, después de ocho años de trabajo en solitario, el 11 de noviembre de 2002, Perelman publicó un preprint de 39 páginas, The entropy formula for the Ricci flow and its geometric applications, anunciando una demostración de la Conjetura de Geometrización de Thurston, propuesta por el matemático William Thurston en 1946 y que implica a la de Poincaré. Más tarde, el 10 de marzo de 2003 publicó un segundo preprint de 22 páginas con el título Ricci flow with surgery on three−manifolds en el que hace algunas mejoras a su trabajo del 11 de noviembre.

Los días 7, 9 y 11 de abril de 2003, realizó un ciclo de conferencias en el Massachussets Institute of Technology, titulado Ricci Flow and Geometrization of Three−Manifolds. Esta fue la primera discusión pública de Perelman sobre los resultados contenidos en sus dos preprints expuestos en arXiv. A las conferencias asistieron más de cien matemáticos incluidos los de más prestigio internacional como John Nash, premio Nobel que inspiró la película “Una Mente maravillosa” y Andrew Wiles que probó el Último Teorema de Fermat.

Grigori Perelman presenta su demostración de  la Conjetura de Geometrización de Thurston

El 15 de abril de 2003, en su sección Ciencia, el periódico New York Times dio a conocer al mundo la noticia sobre la demostración propuesta por Perelman en un reportaje titulado Celebrated Math Problem Solved, Russian Reports.

El mismo 15 de abril, el acontecimiento fue reseñado en MathWorld Headline News, la sección de noticias de Eric Weisstein's World of Mathematics con el título Poincaré Conjecture Proved — This Time for Real.

El 17 de abril The Daily Princetonian publicó la noticia titulándola Perelman explains proof to famous math mystery.

El 20 de abril, en su edición dominical, el New York Times retomó la historia en la sección Week in Review bajo el título A Mathematician's World of Doughnuts and Spheres.

El 7 de mayo, la BBC, en su edición online de BBC News, se refirió al tema bajo el titular Great maths puzzle 'solved'.

Para poder optar a la medalla Fields es necesario que se publique el trabajo en una revista científica y supere dos años de revisiones de la comunidad matemática. No obstante, James Carlson, presidente del Instituto Clay afirmó que, aunque el trabajo había sido publicado en Internet, podría optar al premio si transcurrido el plazo anteriormente mencionado no se encontraba fallo alguno en su demostración.

El 5 de junio de 2006 los matemáticos chinos Zhu Xiping y Cao Huaidong anunciaron la demostración completa basándose en los trabajos preliminares de Perelman (éstos sí publicados en revistas especializadas), lo que, una vez realizada su validación por la comunidad matemática, daría fin a la clasificación completa de las estructuras topológicas de dimensión tres o tridimensionales. Sin embargo, una gran parte de la comunidad matemática pensó que la demostración correspondía a Perelman y consideró el trabajo de los matemáticos chinos como un plagio.

La Conjetura de Poincaré es uno de los problemas más importantes de la Topología Geométrica; podríamos medir esta importancia por la gran cantidad de intentos fallidos realizados por los matemáticos a lo largo de la historia para demostrarla, incluido el propio Poincaré y por la enorme producción de artículos sobre la cuestión, hasta el punto que Brittenham se refiere a este interés irrefrenable como la enfermedad de Poincaritis: una vez enfermos, continúan tratando de probar la conjetura de Poincaré durante aproximadamente 20 años. Ha habido una gran cantidad de topólogos famosos que han sido atacados por esta enfermedad (...) como R. H. Bing, John Stallings, John Hempel, y C. D. Papakyriakopoulos.

Un teorema es una proposición, una afirmación, que hay que demostrar. Si no se ha demostrado, es una “simple” conjetura. Así era la de Poincaré antes de ser demostrada por Perelman, era una afirmación topológica hecha por uno de los más importantes matemáticos de la historia. Pero, ¿qué es la topología?.

La Topología es una disciplina que estudia las propiedades de las superficies que no son alteradas por deformaciones continuas; este concepto topológico puede explicarse de manera intuitiva si consideramos los objetos hechos de un material elástico, que puede ser estirado, contraído o retorcido, pero no rasgado ni roto. Con este criterio un plano puede deformarse hasta convertirse en un paraboloide de revolución, un balón hinchado o deshinchado en un elipsoide, la superficie de la Tierra o de una manzana en una esfera... Para la Topología estas superficies son homeomorfas (esencialmente iguales). En cambio, un donut no puede deformarse de la forma descrita anteriormente para convertirse en una esfera.

Dicho de otra forma, la topología se ocupa de aquellas propiedades de las figuras que permanecen invariantes, cuando dichas figuras son plegadas, dilatadas, contraídas o deformadas, de modo que no aparezcan nuevos puntos, o se hagan coincidir puntos diferentes. La transformación permitida presupone, en otras palabras, que hay una correspondencia biunívoca entre los puntos de la figura original y los de la transformada, y que la deformación hace corresponder puntos próximos a puntos próximos. Esta última propiedad se llama continuidad, y lo que se requiere es que la transformación y su inversa sean ambas continuas: así, trabajamos con homeomorfismos.

El topólogo considera los mismos objetos que el geómetra, pero de modo distinto: no se fija en las distancias o los ángulos, ni siquiera de la alineación de los puntos. Para el topólogo un círculo es equivalente a una elipse; una bola no se distingue de un cubo: se dice que la bola y el cubo son objetos topológicamente equivalentes, porque se pasa de uno al otro mediante una transformación continua y reversible.

Un chiste habitual entre los matemáticos que se dedican a la topología es que «un topólogo es una persona incapaz de distinguir una taza de una rosquilla».

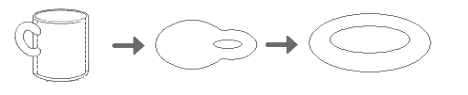
Observemos la siguiente imagen:

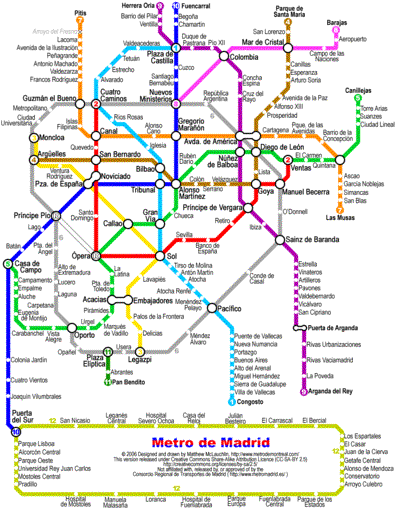
Es un plano del metro de Madrid. Aquí están representadas las estaciones y las líneas de metro que las unen. Pero no es geométricamente exacto. La curvatura de las líneas de metro no coincide, ni su longitud a escala, ni la posición relativa de las estaciones... Pero aun así es un plano perfectamente útil (de hecho, si fuera exacto sería bastante más difícil de utilizar). Sin embargo este plano es exacto en cierto sentido; representa fielmente cierto tipo de información, la única que necesitamos para decidir nuestro camino por la red de metro: información topológica.

El objetivo de la topología es la clasificación de los objetos matemáticos a través de su caracterización, que es el conjunto de propiedades que los definen sin ambigüedad (recuerdo que un topólogo considera dos objetos esencialmente iguales cuando son homeomorfos, lo cual quiere decir que uno se puede transformar en otro, sin romperse y de forma continua).

Volviendo al enunciado de La conjetura de Poincaré, voy a tratar de explicar los conceptos que ahí aparecen:

·        3-variedad o variedad de dimensión 3. Variedad es una generalización de curvas y superficies a espacios de mayor dimensión. Una curva en el plano R² (recta, parábola,...) es una 1-variedad; una superficie en R³ (esfera, cilindro,...) es una 2-variedad, y así sucesivamente. Por tanto, una 3-variedad es un objeto matemático de R⁴, un espacio de 4 dimensiones. Una cosa, en todos los objetos se consideran sólo sus bordes, por ejemplo, en el caso de la esfera sólo consideramos la superficie externa, no se trata de una bola maciza.

·        Cerrada. Compacta, con una extensión finita, como La Tierra, donde si caminas alrededor de ella, por fuerza regresas al punto de partida.

• Simplemente conexa. De forma intuitiva, viene a decir que la variedad no tiene agujeros. Por ejemplo, la 2-variedad S² (la esfera tal y como todos la conocemos) es simplemente conexa, pero la 2-variedad T (un toro) no lo es, ya que tiene un agujero en medio.

·        Homeomorfa. Topológicamente iguales, por ejemplo, una circunferencia y una elipse (1-variedades) son homeomorfas ya que puedo deformar cada una de ellas (sin romperlas) y transformarlas en la otra.

Y ahora vamos a intentar explicarlo geométricamente. El resultado quiere decir más o menos algo así (lo haremos con 2-variedades, es decir, figuras en 3 dimensiones, ya que éstas sí las podemos ver con facilidad).Tenemos una esfera:                                           

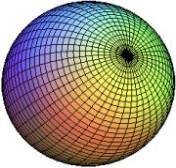
Supongamos que cogemos una cuerda, rodeamos la esfera con ella (por ejemplo por el ecuador de la misma, aunque podría ser por cualquier otro sitio) y le hacemos un nudo corredizo. Ahora tiramos del extremo de la cuerda. ¿Qué pasa?. Pues que la cuerda deslizará por la superficie y poco a poco la circunferencia que formaba al principio se hará cada vez más pequeña hasta que en la parte superior o inferior de la esfera será como un punto. Y esto pasa con cualquier curva cerrada situada en cualquier parte de la esfera. Esto es a grandes rasgos el significado de simplemente conexo.

Intentemos hacer lo mismo con un toro, 2-variedad que no es simplemente conexa:

Supongamos que situamos la cuerda rodeando el toro en perpendicular a la figura. Si tiráramos de ella no pasaría lo mismo que en el caso anterior, seguiría siendo de la misma forma y del mismo tamaño, y lo mismo ocurriría si moviéramos la cuerda alrededor del toro.

Si rodeamos el toro en paralelo a la figura y tiramos de la cuerda sí conseguiremos deformarla, pero debido al agujero que el toro tiene en medio no podremos conseguir que la cuerda llegue a ser un punto, como en el caso anterior. Cuando llegáramos al borde interno no podríamos seguir. De esta forma podemos ver que efectivamente el toro es una 2-variedad que no es simplemente conexa.

Al estar demostrada la generalización de la conjetura para n = 2 lo expuesto anteriormente nos dice que las 2-variedades esfera y toro no son homeomorfas. Es decir, que de las propiedades topológicas de una de ellas no podemos sacar información de las propiedades topológicas de la otra, debemos estudiar cada 2-variedad por separado.

Sin embargo, si por ejemplo tomamos un elipsoide

podemos ver que el experimento de la cuerda nos da los mismos resultados que los obtenidos con la esfera. Al ser también el elipsoide una 2-variedad compacta tenemos, por el (en este caso sí) teorema de Poincaré que la esfera S² y el elipsoide son homeomorfos. Esto también se puede ver intuitivamente en este caso, ya que por ejemplo podemos deformar el elipsoide (sin romperlo) y convertirlo en una esfera.

¿Por qué puede ser importante un resultado así?. Ya se dijo antes que dos objetos homeomorfos, o topológicamente iguales, van a  compartir las propiedades topológicas. Si el resultado es cierto, comprobando que una 3-variedad es compacta y simplemente conexa sabremos muchísimas más cosas de ella, ya que las propiedades topológicas de S³ son conocidas, y al ser homeomorfas la otra 3-variedad hereda todas ellas. A simple vista puede parecer sencillo, ya que es normal pensar solamente en 3 dimensiones, es decir, en 2-variedades y en sus representaciones gráficas. El problema viene cuando queremos estudiar cosas que no podemos ver ni representar gráficamente. En estos casos, si necesitamos sacar información sobre un cierto objeto y tenemos teoremas como éste, el trabajo necesario para ello se reduce bastante. Además, este tipo de resultados ayudan a clasificar los objetos. Ahora podemos decir que, topológicamente hablando, sólo hay una 3-variedad compacta y simplemente conexa: la 3-esfera S³, ya que cualquier otra 3-variedad compacta y simplemente conexa es homeomorfa a ella, o dicho de otra forma, la esfera de dimensión 3, en un espacio de dimensión 4, es la única superficie cerrada sin “agujeros”.

El problema se generalizó para espacios de cualquier dimensión (n+1) y, aunque parezca sorprendente, fue demostrada para todas las dimensiones excepto para dimensión 3; Erik Christopher Zeeman para n=5 en1925, Stephen Smale para n≥7 en 1930, John R. Stallings para n=6 en 1962 y Michael Hartley Freedman para n=4 en 1951.

En torno a las aplicaciones prácticas, los grandes matemáticos actuales opinan que, para llegar  hasta ellas, le falta a la tecnología un par de siglos. En cosmología podría tener implicaciones, en cuanto a cuál es la forma del universo o a catalogar todas las formas tridimensionales que en él existan. Pero, para un matemático, la importancia no radica en las futuras aplicaciones, sino en el logro alcanzado por la humanidad.

CAPÍTULO IV

SU CARÁCTER

Grigori "Grisha" Yakovlevich Perelman (en ruso: Григорий Яковлевич Перельман) nació en Leningrado (ahora san Petersburgo) en una familia judía el 13 de junio de 1966. Su educación matemática temprana ocurrió en la Escuela secundaria 239 de Leningrado, una escuela especializada en programas de matemáticas y de física avanzadas. En 1982, como miembro de la URSS, compitiendo en la Olimpiada Internacional de Matemática, (una competencia internacional para estudiantes de bachillerato), ganó la medalla de oro tras alcanzar una puntuación perfecta. A principios de los 80, consiguió la puntuación más alta en la prestigiosa organización Mensa para personas con elevado coeficiente intelectual. Al final de los años ochenta, Perelman adquirió un grado en Candidato de Ciencia (el equivalente ruso del doctorado) en la Facultad de Mecánica y Matemática de la Universidad del Estado de Leningrado, una de las universidades líderes de la ex-Unión Soviética. Su disertación se llamó "Superficies en silla en espacios euclídeos". Era también un talentoso violinista y jugaba tenis de mesa.

Después de la graduación, Perelman comenzó a trabajar en Leningrado en el renombrado Instituto Steklov de Matemáticas de la Academia Rusa de las Ciencias. Sus asesores en el Instituto Steklov fueron Aleksandr Danilovich Aleksandrov y Yuri Dmitrievich Burago. Al final de los ochenta y principios de los noventa, Perelman tenía puestos en varias universidades de Estados Unidos. En 1992, fue invitado a pasar sendos semestres en la Universidad de Nueva York y en la Universidad de Stony Brook. De allí, aceptó una beca de dos años en la Universidad de California, Berkeley, en 1993. Volvió al Instituto Steklov en el verano de 1995, donde trabajó incansablemente en la demostración de la Conjetura de Geometrización de Thurston, propuesta por el matemático William Thurston en 1946.

En 2002 y 2003 publicó electrónicamente la demostración de la Conjetura de Poincaré, y su fama se extendió por todo el universo matemático.

En agosto de 2006, rechazó la medalla Fields, la más prestigiosa recompensa mundial, que le fue concedida, junto a otros tres laureados, en el marco del XXV Congreso Internacional de Matemáticos (CIM) celebrado en Madrid. A partir de aquí, su fama se ha extendido rapidísimamente por todo el mundo, no sólo por haber rechazado el premio de la Unión Matemática Internacional (más bien simbólico, de 9.500 euros), sino también, y sobre todo, por haberlo hecho con respecto al millón de dólares que el Instituto Clay de Matemáticas de Cambridge (Massachussets) prometió al que resolviese la conjetura planteada, en 1904, por Poincaré. No era la primera vez que rechazaba un premio; en 1996, no aceptó el del Congreso Europeo de Matemáticas.

Todo el mundo matemático deseaba ver al genio ruso recibiendo la medalla de manos del monarca español. Pero, no acudió a la cita.

"No le diré nada (...) ni siquiera por qué me niego a hablar del premio", declaró Perelman al ser contactado telefónicamente en San Petersburgo."Llámeme dentro de unos meses", añadió el matemático sin que quedara claro si estaba hablando en serio o sólo tratando de librarse del periodista.

El Instituto de matemáticas Steklov de San Petersburgo, donde Grigori Perelman fue investigador hasta que renunció en enero, consideró el premio como un "evento extraordinario" y explicó la negativa del sabio a recibir la distinción por su carácter "original".Las personas como él "son originales", estimó Anatoli Verchtchik, presidente de la Unión de Matemáticos de San Petersburgo y profesor del Instituto, antes de subrayar que no podía precisar "dónde termina la originalidad y dónde comienza otra cosa".

Se dice que sus amigos han afirmado que él encuentra actualmente a las matemáticas un tema doloroso para discutir; algunos dicen incluso que ha abandonado las matemáticas por completo. De acuerdo a una entrevista reciente, Perelman está actualmente desempleado viviendo con su madre en San Petersburgo.

Aunque Perelman dice en un artículo en The New Yorker que está decepcionado de los estándares éticos del campo de las matemáticas, el artículo sugiere que Perelman se refiere particularmente a los esfuerzos de Yau por aminorar su papel en la demostración y exaltar el trabajo de Cao y Zhu. También añadió: "no puedo decir que estoy indignado. Otras personas hacen cosas peores. Por supuesto, hay muchos matemáticos que son más o menos honestos. Pero de ellos, casi todos son conformistas. Son más o menos honestos pero toleran a quienes no son honestos";  "no es la gente que rompe los estándares éticos quienes se consideran extraños. Es gente como yo quienes son aislados”.

Esto, combinado con la posibilidad de ser premiado con una medalla Fields, hizo que renunciara a la matemática profesional. Ha dicho que "mientras no era conspicuo, tenía elección, incluso de hacer algo feo (un escándalo sobre la falta de integridad de la comunidad matemática). Ahora, cuando me he vuelto una persona muy conspicua, no puedo ser una mascota y decir nada. Es por esto que tuve que renunciar".

El profesor Marcus du Sautoy de la Universidad de Oxford ha dicho que “él se ha aislado, de cierta manera, de la comunidad matemática. Se ha desilusionado de las matemáticas, lo cual es muy lamentable. No está interesado en el dinero. El gran premio para él es demostrar su teorema”.

John Ball, presidente del Comité de las Medallas Fields, dijo en rueda de prensa que pasó dos días en San Petersburgo intentando baldíamente convencer a Perelman para que aceptara el galardón.

Ball dijo que su rechazo "se centraba en sus sentimientos de aislamiento frente a la comunidad matemática"."Consecuentemente, no quiere ser una figura simbólica de esa comunidad. Obviamente, tiene una psicología diferente a la de otra gente".

Un amigo de Perelman, Anatoly Vershik, dijo que el matemático sólo estaba interesado en que su trabajo fuera declarado correcto, y que consideraba cualquier otra forma de reconocimiento "superficial"."Es un tema muy personal, que puede tener su lógica, o quizás no", dijo Vershik, presidente de la Sociedad Matemática de San Petersburgo, a Reuters en un comunicado. "Es muy reservado, no quiere hablar de ello", añadió.

Según la prestigiosa revista Science, el avance científico más importante de 2006 ha sido la resolución de la Conjetura de Poincaré.

Después de todo esto, se puede decir que Grisha es, para la mayoría de la gente, más bien un personaje literario creado por los medios de comunicación en una época del año, agosto, en la que surgen pocas noticias, víctima de un gesto inusual en este mundo actual como es el de renunciar a un premio metálico muy importante (¿qué hubieran elucubrado si aún existiera el Telón de Acero?). Pero, para los matemáticos, el logro no tiene precio, no hay dinero en este planeta para pagar una hazaña científica como la realizada por el Doctor Perelman; ni siquiera nos cuestionamos las importantísimas aplicaciones futuras que pueda tener su demostración, ése es un trabajo para nuestros primos, los físicos. ¡VIVA LA MATEMÁTICA!

Autor: Miguel Bandera Ruiz

I.E.S. Bezmiliana

Fuentes:

http://es.wikipedia.org

http://www.matematicas.profes.net

http://www.foroswebgratis.com

www.elmundo.es

http://nacho.unicauca.edu.co

Perelman, G., The entropy formula for the Ricci flow and its geometric applications, arXiv e–Print Archive, 11 de noviembre de 2002.

Perelman, G., Ricci flow with surgery on three–manifolds, arXiv e–Print Archive, 10 de marzo de 2003.

http://gaussianos.blogsome.com