CAPÍTULO III
LA CONJETURA DE Poincaré

Henri Poncaré (1904):
“Toda variedad de dimensión 3 cerrada y simplemente conexa es homeomorfa a la esfera de dimensión tres”
¡POR FAVOR, NO CIERRE LA PÁGINA. TRATARÉ DE EXPLICÁRSELO LO MEJOR POSIBLE!.
El enunciado no pudo ser resuelto durante un siglo y su demostración fue considerada uno de Los siete problemas del Milenio propuestos por el Clay Mathematics Institute.
En noviembre de 2002 corrió el rumor en Internet de que Grigori Perelman (“Grisha”) había publicado en arXiv una solución a la Conjetura; arXiv es un sistema electrónico y automático de distribución de artículos de investigación (preprint) en diversos campos (física, matemáticas, etc.) sin revisión editorial, lo que reduce ampliamente el coste.
En efecto, después de ocho años de trabajo en solitario, el 11 de noviembre de 2002, Perelman publicó un preprint de 39 páginas, The entropy formula for the Ricci flow and its geometric applications, anunciando una demostración de la Conjetura de Geometrización de Thurston, propuesta por el matemático William Thurston en 1946 y que implica a la de Poincaré. Más tarde, el 10 de marzo de 2003 publicó un segundo preprint de 22 páginas con el título Ricci flow with surgery on three−manifolds en el que hace algunas mejoras a su trabajo del 11 de noviembre.
Los días 7, 9 y 11 de abril de 2003, realizó un ciclo de conferencias en el Massachussets Institute of Technology, titulado Ricci Flow and Geometrization of Three−Manifolds. Esta fue la primera discusión pública de Perelman sobre los resultados contenidos en sus dos preprints expuestos en arXiv. A las conferencias asistieron más de cien matemáticos incluidos los de más prestigio internacional como John Nash, premio Nobel que inspiró la película “Una Mente maravillosa” y Andrew Wiles que probó el Último Teorema de Fermat.
Grigori Perelman presenta su demostración de la Conjetura de Geometrización de Thurston
El 15 de abril de 2003, en su sección Ciencia, el periódico New York Times dio a conocer al mundo la noticia sobre la demostración propuesta por Perelman en un reportaje titulado Celebrated Math Problem Solved, Russian Reports.
El mismo 15 de abril, el acontecimiento fue reseñado en MathWorld Headline News, la sección de noticias de Eric Weisstein's World of Mathematics con el título Poincaré Conjecture Proved — This Time for Real.
El 17 de abril The Daily Princetonian publicó la noticia titulándola Perelman explains proof to famous math mystery.
El 20 de abril, en su edición dominical, el New York Times retomó la historia en la sección Week in Review bajo el título A Mathematician's World of Doughnuts and Spheres.
El 7 de mayo, la BBC, en su edición online de BBC News, se refirió al tema bajo el titular Great maths puzzle 'solved'.
Para poder optar a la medalla Fields es necesario que se publique el trabajo en una revista científica y supere dos años de revisiones de la comunidad matemática. No obstante, James Carlson, presidente del Instituto Clay afirmó que, aunque el trabajo había sido publicado en Internet, podría optar al premio si transcurrido el plazo anteriormente mencionado no se encontraba fallo alguno en su demostración.
El 5 de junio de 2006 los matemáticos chinos Zhu Xiping y Cao Huaidong anunciaron la demostración completa basándose en los trabajos preliminares de Perelman (éstos sí publicados en revistas especializadas), lo que, una vez realizada su validación por la comunidad matemática, daría fin a la clasificación completa de las estructuras topológicas de dimensión tres o tridimensionales. Sin embargo, una gran parte de la comunidad matemática pensó que la demostración correspondía a Perelman y consideró el trabajo de los matemáticos chinos como un plagio.
La Conjetura de Poincaré es uno de los problemas más importantes de la Topología Geométrica; podríamos medir esta importancia por la gran cantidad de intentos fallidos realizados por los matemáticos a lo largo de la historia para demostrarla, incluido el propio Poincaré y por la enorme producción de artículos sobre la cuestión, hasta el punto que Brittenham se refiere a este interés irrefrenable como la enfermedad de Poincaritis: una vez enfermos, continúan tratando de probar la conjetura de Poincaré durante aproximadamente 20 años. Ha habido una gran cantidad de topólogos famosos que han sido atacados por esta enfermedad (...) como R. H. Bing, John Stallings, John Hempel, y C. D. Papakyriakopoulos.

Un teorema es una proposición, una afirmación, que hay que demostrar. Si no se ha demostrado, es una “simple” conjetura. Así era la de Poincaré antes de ser demostrada por Perelman, era una afirmación topológica hecha por uno de los más importantes matemáticos de la historia. Pero, ¿qué es la topología?.
La Topología es una disciplina que estudia las propiedades de las superficies que no son alteradas por deformaciones continuas; este concepto topológico puede explicarse de manera intuitiva si consideramos los objetos hechos de un material elástico, que puede ser estirado, contraído o retorcido, pero no rasgado ni roto. Con este criterio un plano puede deformarse hasta convertirse en un paraboloide de revolución, un balón hinchado o deshinchado en un elipsoide, la superficie de la Tierra o de una manzana en una esfera... Para la Topología estas superficies son homeomorfas (esencialmente iguales). En cambio, un donut no puede deformarse de la forma descrita anteriormente para convertirse en una esfera.
Dicho de otra forma, la topología se ocupa de aquellas propiedades de las figuras que permanecen invariantes, cuando dichas figuras son plegadas, dilatadas, contraídas o deformadas, de modo que no aparezcan nuevos puntos, o se hagan coincidir puntos diferentes. La transformación permitida presupone, en otras palabras, que hay una correspondencia biunívoca entre los puntos de la figura original y los de la transformada, y que la deformación hace corresponder puntos próximos a puntos próximos. Esta última propiedad se llama continuidad, y lo que se requiere es que la transformación y su inversa sean ambas continuas: así, trabajamos con homeomorfismos.
El topólogo considera los mismos objetos que el geómetra, pero de modo distinto: no se fija en las distancias o los ángulos, ni siquiera de la alineación de los puntos. Para el topólogo un círculo es equivalente a una elipse; una bola no se distingue de un cubo: se dice que la bola y el cubo son objetos topológicamente equivalentes, porque se pasa de uno al otro mediante una transformación continua y reversible.
Un chiste habitual entre los matemáticos que se dedican a la topología es que «un topólogo es una persona incapaz de distinguir una taza de una rosquilla».
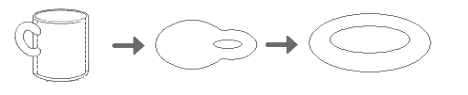
Observemos la siguiente imagen:
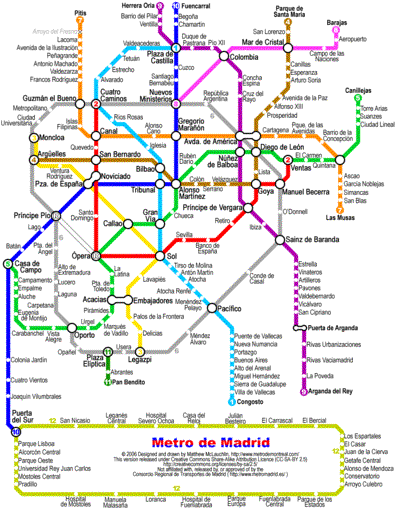
Es un plano del metro de Madrid. Aquí están representadas las estaciones y las líneas de metro que las unen. Pero no es geométricamente exacto. La curvatura de las líneas de metro no coincide, ni su longitud a escala, ni la posición relativa de las estaciones... Pero aun así es un plano perfectamente útil (de hecho, si fuera exacto sería bastante más difícil de utilizar). Sin embargo este plano es exacto en cierto sentido; representa fielmente cierto tipo de información, la única que necesitamos para decidir nuestro camino por la red de metro: información topológica.
El objetivo de la topología es la clasificación de los objetos matemáticos a través de su caracterización, que es el conjunto de propiedades que los definen sin ambigüedad (recuerdo que un topólogo considera dos objetos esencialmente iguales cuando son homeomorfos, lo cual quiere decir que uno se puede transformar en otro, sin romperse y de forma continua).
Volviendo al enunciado de La conjetura de Poincaré, voy a tratar de explicar los conceptos que ahí aparecen:
· 3-variedad o variedad de dimensión 3. Variedad es una generalización de curvas y superficies a espacios de mayor dimensión. Una curva en el plano R2 (recta, parábola,...) es una 1-variedad; una superficie en R3 (esfera, cilindro,...) es una 2-variedad, y así sucesivamente. Por tanto, una 3-variedad es un objeto matemático de R4, un espacio de 4 dimensiones. Una cosa, en todos los objetos se consideran sólo sus bordes, por ejemplo, en el caso de la esfera sólo consideramos la superficie externa, no se trata de una bola maciza.
· Cerrada. Compacta, con una extensión finita, como La Tierra, donde si caminas alrededor de ella, por fuerza regresas al punto de partida.
- Simplemente conexa. De forma intuitiva, viene a decir que la variedad no tiene agujeros. Por ejemplo, la 2-variedad S2 (la esfera tal y como todos la conocemos) es simplemente conexa, pero la 2-variedad T (un toro) no lo es, ya que tiene un agujero en medio.
· Homeomorfa. Topológicamente iguales, por ejemplo, una circunferencia y una elipse (1-variedades) son homeomorfas ya que puedo deformar cada una de ellas (sin romperlas) y transformarlas en la otra.
Y ahora vamos a intentar explicarlo geométricamente. El resultado quiere decir más o menos algo así (lo haremos con 2-variedades, es decir, figuras en 3 dimensiones, ya que éstas sí las podemos ver con facilidad).Tenemos una esfera:
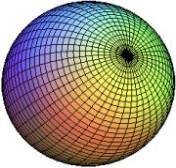
Supongamos que cogemos una cuerda, rodeamos la esfera con ella (por ejemplo por el ecuador de la misma, aunque podría ser por cualquier otro sitio) y le hacemos un nudo corredizo. Ahora tiramos del extremo de la cuerda. ¿Qué pasa?. Pues que la cuerda deslizará por la superficie y poco a poco la circunferencia que formaba al principio se hará cada vez más pequeña hasta que en la parte superior o inferior de la esfera será como un punto. Y esto pasa con cualquier curva cerrada situada en cualquier parte de la esfera. Esto es a grandes rasgos el significado de simplemente conexo.
Intentemos hacer lo mismo con un toro, 2-variedad que no es simplemente conexa:

Supongamos que situamos la cuerda rodeando el toro en perpendicular a la figura. Si tiráramos de ella no pasaría lo mismo que en el caso anterior, seguiría siendo de la misma forma y del mismo tamaño, y lo mismo ocurriría si moviéramos la cuerda alrededor del toro.
Si rodeamos el toro en paralelo a la figura y tiramos de la cuerda sí conseguiremos deformarla, pero debido al agujero que el toro tiene en medio no podremos conseguir que la cuerda llegue a ser un punto, como en el caso anterior. Cuando llegáramos al borde interno no podríamos seguir. De esta forma podemos ver que efectivamente el toro es una 2-variedad que no es simplemente conexa.
Al estar demostrada la generalización de la conjetura para n = 2 lo expuesto anteriormente nos dice que las 2-variedades esfera y toro no son homeomorfas. Es decir, que de las propiedades topológicas de una de ellas no podemos sacar información de las propiedades topológicas de la otra, debemos estudiar cada 2-variedad por separado.
Sin embargo, si por ejemplo tomamos un elipsoide

podemos ver que el experimento de la cuerda nos da los mismos resultados que los obtenidos con la esfera. Al ser también el elipsoide una 2-variedad compacta tenemos, por el (en este caso sí) teorema de Poincaré que la esfera S2 y el elipsoide son homeomorfos. Esto también se puede ver intuitivamente en este caso, ya que por ejemplo podemos deformar el elipsoide (sin romperlo) y convertirlo en una esfera.
¿Por qué puede ser importante un resultado así?. Ya se dijo antes que dos objetos homeomorfos, o topológicamente iguales, van a compartir las propiedades topológicas. Si el resultado es cierto, comprobando que una 3-variedad es compacta y simplemente conexa sabremos muchísimas más cosas de ella, ya que las propiedades topológicas de S3 son conocidas, y al ser homeomorfas la otra 3-variedad hereda todas ellas. A simple vista puede parecer sencillo, ya que es normal pensar solamente en 3 dimensiones, es decir, en 2-variedades y en sus representaciones gráficas. El problema viene cuando queremos estudiar cosas que no podemos ver ni representar gráficamente. En estos casos, si necesitamos sacar información sobre un cierto objeto y tenemos teoremas como éste, el trabajo necesario para ello se reduce bastante. Además, este tipo de resultados ayudan a clasificar los objetos. Ahora podemos decir que, topológicamente hablando, sólo hay una 3-variedad compacta y simplemente conexa: la 3-esfera S3, ya que cualquier otra 3-variedad compacta y simplemente conexa es homeomorfa a ella, o dicho de otra forma, la esfera de dimensión 3, en un espacio de dimensión 4, es la única superficie cerrada sin “agujeros”.
El problema se generalizó para espacios de cualquier dimensión (n+1) y, aunque parezca sorprendente, fue demostrada para todas las dimensiones excepto para dimensión 3; Erik Christopher Zeeman para n=5 en1925, Stephen Smale para n≥7 en 1930, John R. Stallings para n=6 en 1962 y Michael Hartley Freedman para n=4 en 1951.
En torno a las aplicaciones prácticas, los grandes matemáticos actuales opinan que, para llegar hasta ellas, le falta a la tecnología un par de siglos. En cosmología podría tener implicaciones, en cuanto a cuál es la forma del universo o a catalogar todas las formas tridimensionales que en él existan. Pero, para un matemático, la importancia no radica en las futuras aplicaciones, sino en el logro alcanzado por la humanidad.
